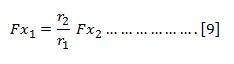EJEMPLO DE MODELADO DE SISTEMAS HIBRIDOS.

Modelar el siguiente sistema mostrado en la figura 1, en función de  “x₂”.

 

Figura 1.

Solución:

Primeramente hacemos el D.C.L para la masa m2     (figura 2).

Figura 2.

Figura 2.

Entonces decimos que

 

Aplicando las ecuaciones de equilibrio

Obteniendo el modelo matemático.

 

Tomando la masa m₁ y sacamos el D.C.L. (figura 3).

Figura 3.

Entonces decimos que

 

Aplicando las ecuaciones de equilibrio

 

Obteniendo el modelo matemático.

Estableciendo ecuaciones de acoplamiento.

 pero

entonces relacionando 3 y 4

Sustituyendo la ecu. 5 en la ecu. 2 

 

Tomando en cuenta los pares aplicados  a la palanca.

pero

entonces relacionando 7 y 8

 

Sustituyendo la ecuación 9 en la ecuación 6.

Por la ecuación 1.

Finalmente tenemos.

  

ejemplo 2: obtener el modelo matematico de un sistema mecanico traslacional

Obtener el modelo matemático mostrado en la figura 2 en función de m₁ y m₂

                                                                   

                                                                    Figura 2

Solución:

Primeramente hacemos el D.C.L para la masa m₁

_.

                                                                  Figura 2.1

Entonces decimos que

 

Obteniendo el modelo matemático.

                                       

Tomando la segunda masa m₂ y sacamos el D.C.L.

                                                                 Figura 2.2

Entonces decimos que

             

 

                                           

Por lo tanto el modelo matematico es

Ejemplo de Modelado de un Sistema Mecánico.

Ejemplo.

Obtener las ecuaciones de equilibrio del sistema mecánico rotacional formado por un resorte rotacional, un amortiguador rotacional o torsional y una inercia, como se muestra en la figura 1.

                                                                  Figura 1.

Solución:

Diagrama de Cuerpo Libre figura 2.

 

                                                                       Figura 2

Entonces:

Esta sería la ecuación de equilibrio del sistema.